TUNING
Robert Hollingworth's guide for choral singers
—
Having been a boy chorister, I thought I knew how to tune but more recently I’ve become more aware why intervals sound in tune and have put this into practice with I Fagiolini - also on the MA at the University of York. If science isn’t your thing, don’t be deterred: it quickly becomes common sense, one solution reinforcing another.
The basic premise is that what makes an interval ‘in tune’ is how close it sounds to the natural intervals of the harmonic series. Sing like this (sometimes called Just Intonation) and the music feels like a perfectly tailored suit.

Unfortunately, the pianos/organs we tend to practise alongside are in a compromise tuning system called equal temperament in which everything except the octave is a little bit out of tune.

I’ve tried to keep things simple, to show what I mean through sound samples and I recommend you watch this clip first - which also contains a poor-quality car hire/tuning gag.
Clip 1
MAJOR 3RDS
In a chord (we’re not dealing with melodic intervals yet, just the intervals between notes in a chord), pure major 3rds are narrower than we find on the piano’s compromise system of tuning. These pure major 3rds are found between the 4th and 5th steps of the harmonic series, a series in which the successive notes are multiples of the number of vibrations per second (Hertz) of the fundamental note (you find this series all over nature - mathematicians love them). Here’s the start of one in A major which is nice and simple because of the round numbers involved.

Fig. 1
Because it’s simpler to explain in C major, here’s the start of the harmonic series on C. (It has awkward numbers of Hertz so we’ll leave that detail out as the proportions are the same for any fundamental - and just keep the intervals and their number in the series.)

Fig. 2
We are trying to sing all our major 3rds as close as possible to the natural major 3rd found between C and E – harmonics 4 and 5. If we get it right there will be no beating or interference between the two notes and the world will seem a beautiful place.
This is the sound of a pure major 3rd according to that pure ratio of the 4th and 5th degrees of a harmonic series based on C (so a C and an E).
Sound Clip 1
Now hear an equal tempered (piano) third gradually changing into the pure one as the top note is fractionally lowered. Feel it come into focus!
Sound Clip 1a
The major 3rds in a scale of C major are C-E F-A G-B. Only the first of these is easily found in the table above but the principle is the same whenever you sing a major 3rd.
MINOR 3RDS
Pure minor 3rds are wider than piano minor 3rds. We’re trying to sing a pure minor 3rd as found between the 5th and 6th steps of the harmonic series.
Sound Clip 2
This will sound VERY bright/wide to many ears! The proof is adding the major 3rd below it to make a major chord: the 4th, 5th and 6th degrees of the harmonic series.
Sound Clip 3
The minor 3rds in a scale of C major are D-F E-G A-C B-D.
MAJOR CHORDS
Take a C major triad which contains within it the perfect 5th C-G, a major 3rd C-E and a minor 3rd E-G.

Fig. 3
When you lower the E to make the C-E major 3rd pure, the pulling down of that E simultaneously puts it into the right place for it (the E) to make a wider minor 3rd with the G. Everything lines up.
Here’s the whole chord pure according the harmonic series
numbers 4, 5 and 6.
Sound Clip 4
And here is the normal equal temperament version slowly changing into that pure version! Can you hear that 'beating' gradually disappear?
Sound Clip 5
Of course we are only using the terms ‘lowering’ and ‘raising’ in comparison to the equal temperament we have got used to.
MINOR CHORDS
Let’s use D minor.

Fig. 3a
In minor chords the minor 3rd is on the bottom – in D minor, D-F.
When you raise the F to make the D-F minor 3rd wider/pure, it also pops the F into the right place for it to be a narrow major 3rd with the A. Listen to the minor third changing from equal tempered to pure.
Sound Clip 6
Now here's that whole minor triad changing from equal tempered to pure.
Sound Clip 7
SOME HELPFUL CHEATS
So far we’ve only looked at chords but of course we sing melodies and move from one note to another. What rules of thumb when singing melodies would be useful to end up in the right place for the tuning of the chords?
SINGING SEMITONES IN A MELODY
In a major key, we now know that the third degree – in C major an E - is lower than the piano if it's to be a pure major 3rd to C. As the E is lower, that means that when you move from F-E, the semitone will have to be a little wider than usual.
The other semitone in any major scale is the 7th to 8th degree: in C major B-C. Similarly the B will have been lowered to be a pure major 3rd to the G, which means it’s a bigger stretch than we’re used to in order to reach it from the C.
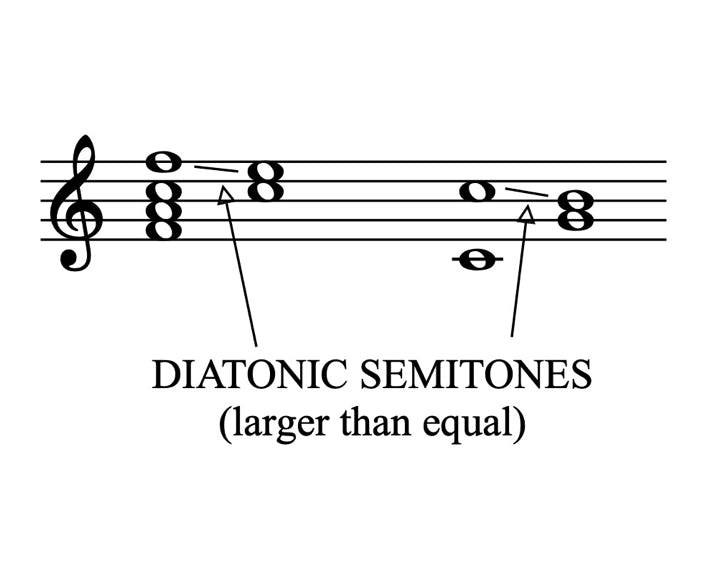
Fig. 4
Melodic Semitone Sample
Sound Clip 8
Any major scale has these two semitones between its 3rd and 4th degrees and its 7th and 8th. They will always need to be sung wide. We’re going to give these a name – DIATONIC SEMITONES. They’re wider than a normal semitone by about a 6th of a piano semitone. That sounds like nothing but you can feel the difference.
To think of it another way, imagine the notes of a scale like people sitting on a row of seats in the underground: diatonic semitones MAN-SPREAD and take up more of the available octave than equal temperament ones, leaving less room for other intervals.

Fig. 6
The manspreader is E-F. And the passenger on the left is the tone below
(D-E) and has to bunch up a bit - so it's a smaller tone than we’re used to. This makes sense because that is how we get to the narrower major 3rd we need. C-D ('normal' tone) + D-E ('small' tone) = narrow major 3rd.
Exactly the same principles occur in a minor key (and modes) but on different degrees from the major.
In minor keys, the semitones are between the 2nd and 3rd degrees: in C minor, this means D-Eb and the 5th and 6th: G-Ab. In both cases the top note will either be sitting on top of a minor 3rd: C-Eb or F-Ab (minor 3rds need to be high so the flat will be high) – or you can look at it another way, with the Bb (or other flat note) needing to be high because it then makes a nice narrow major 3rd with the note above: Ab-C Eb-G Bb-D. So singing wide diatonic semitones to get those flats high still works.
CHROMATIC SEMITONES
What about the other type of semitone when the letter in the note name stays the same: F-F# or B-Bb? These are called CHROMATIC semitones and are narrower than equal temperament (piano) semitones.
Keeping chromatic semitones narrow is a helpful way to think in melodic terms when we're singing a piece of music. But the harmonic logic for this is: C# sits at the top of a major 3rd (A-C#). The C# must be low to make the major 3rd pure.
Sound Clip 9
C natural sits at the top of a minor 3rd (A-C). The C must be high to make the minor 3rd pure.
Sound Clip 10
Result :
C natural to C# (chromatic semitone) needs to be small to achieve this.
Sound Clip 11
SHARPS AND FLATS (another cheat)
Something rather counter-intuitive is becoming apparent.
Flat notes are often the top note of a minor 3rd: C-Eb F-Ab G-Bb. So it’s useful to note that we need to keep our flats high (when they’re functioning as minor 3rds).
What about sharps? Their function is often to be on the top of a major 3rd – D-F# E-G# A-C# B-D# - so we’ll be keeping them low for the major 3rd to be narrow enough.
Flats high - sharps low? Everything you always knew - except the exact opposite.

Fig. 7
This is just a cheat to help you navigate a score – it only works in keys with a few sharps or flats. It doesn’t work in Gb major for example, because most of the notes of that scale are flats. But it’s useful to bear it in mind.
WHY BOTHER WITH ANY OF THIS?
Because there is a hidden problem with singing in equal temperament. You could just say (and admit it, choir-leaders, you often do) ‘I just like wide major 3rds with and that’s my taste’. That would be fine if it were not for the following.
Within any note we sing, as well as the sung note itself, there resonate within it a whole series of other frequencies – an entire harmonic series. Here’s me trying to isolate some of those notes to make them super-clear.
Clip 2
Can you hear the little arpeggio at the top of the sound? Or perhaps you hear a changing vowel - because that’s exactly what vowels are: different combinations of those harmonics that allow us to differentiate sounds and thus to communicate. Listen to the clip above again.
A group of five singers want to sing a really in tune A major chord with a C# at the top.

Fig. 8
The top voice wants to sing a high (equal tempered) C#. But the bass low A already contains all the notes of the chord within his low A as harmonics - including the C#. You can hear it here.
Clip 3
Even without the top voice singing the C# and just putting in the rest of the chord without it, we can in fact hear that C# harmonic so strongly off the bass note that the chord feels complete.
CLIP COMING SOON
Clip 4
So the top voice needs to sing a C# to match that harmonic – a pure major 3rd - or its higher third will beat against the same C# coming off the Bass A (as its 5th harmonic). If you want the numbers, an equal tempered C# at that pitch is at c.555 Hz and will beat nearly five times per second against the pure one at 550 Hz.
Here is that beating, showing the Bass A at 110Hz, its 5th harmonic at 550Hz and a high third at 555Hz.
Sound Clip 12
This is a good moment humbly to remember that no-one can sing perfectly purely in tune all the time but it is useful to know in principle whether you’re aiming high or low. Remember Indiana Jones and the invisible bridge:
Clip 5
SingTheScore episode guide
In the Bennett and Tomkins SingTheScore episodes we added little arrows to the score indicating where notes need to be a little higher or lower to reach a narrower major 3rd or a wider minor third. So that’s a good practice resource.
A few other issues I’ll come back to when I’ve a moment:
- Why Minor triads can never sound as in tune as major ones
- What are we going to do about 7ths?
- How is this all affected by different vowels?
- Why are pianos tuned in equal temperament if they give wrong intervals.
—
I’m putting this page up as I Fagiolini’s recording of Victoria’s Tenebrae Responsories is released, which I think is a fine example of the singers tuning well, particularly where to place their major or minor 3rd, the intervals that seem to be most important.
THANKS TO:
Jacob Ewens for sound samples https://linktr.ee/jacobewens
Chris Davey for music typesetting
Polyphonic Films for design www.polyphonicfilms.com
Further reading :
Ross Duffin - How equal temperament ruined harmony and why you should care.
Norton, 2006.
And my mum, Julie Hollingworth, who in the 90s wrote a book called ‘Between the lines’ which was an introduction to music theory for adults. She spent an inordinate amount of time trying out phrases on me and others to ensure that what she had written was really clear. I have tried to do the same but welcome comments mail@ifagiolini.com on how I could make it clearer: obviously this page can’t explain every subtlety of the tuning minefield.